Direction of the Vector Calculator

Holds a Master's degree in Data Science / Industrial Engineering, obtained at Stellenbosch University, South Africa. His research investigates using swarm intelligence to solve data clustering and other optimization problems. Will never refuse an offer to play some board games. See full profile

58 people find this calculator helpful

Table of contents

If you want to calculate the direction of a vector, you're in the right place. This calculator finds the direction angle of a vector and calculates a unit vector in this direction.

Vectors are a powerful tool to represent many physical quantities in our physical world. They represent forces, velocities, and many other quantities derived from them.

With this tool, you can find the magnitude and direction angle of any vector.

How do I calculate the direction of a vector?

You can express or calculate the direction of a vector v in two ways:

1. Calculating the direction angle of the vector v. The direction angle is the angle that v forms with the positive x-axis, counting in the counterclockwise direction.
2. Calculating a unit vector in the direction of the same vector. This unit vector is called the direction vector.

How to find the direction angle of the vector?

To calculate the angle θ \theta θ that a 2D vector v ⃗ = ( x , y ) \vec = (x, y) v

= ( x , y ) forms with the horizontal axis, use this equation:

The only problem with this equation is that it doesn't give us the angle about the positive x-axis, but only about the nearest horizontal axis. If your vector lies in the first quadrant of the Cartesian plane, like the vector pointing to P ( 3 , 5 ) P(3, 5) P ( 3 , 5 ) in the image, that's not a problem.

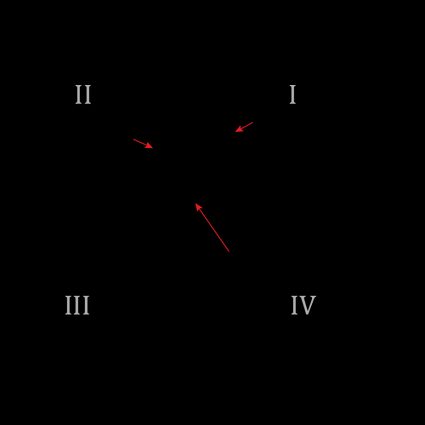
But what if the vector lies in any of the other quadrants? Suppose you want to find the direction angle θ \theta θ of the vector Q = ( − 2 , 4 ) Q = (-2, 4) Q = ( − 2 , 4 ) of the previous image. If we used the previous formula to find the direction angle, we wouldn't obtain the correct angle, as we'd get the angle γ \gamma γ instead of the direction angle θ \theta θ .

How can we deal with this? Well, in this case, you could have noticed that θ = 18 0 ∘ − γ \theta = 180^\circ - \gamma θ = 18 0 ∘ − γ . We can extend this reasoning to the other cases and come up with the following equations to calculate the direction of the vector in each quadrant:

• In the first quadrant, θ I = arctan ⁡ ( y x ) \theta_\text = \arctan(\frac) θ I ​ = arctan ( x y ​ ) .
• In the second quadrant, θ II = 180 ° − arctan ⁡ ( y x ) \theta_\text = 180° - \arctan(\frac) θ II ​ = 180° − arctan ( x y ​ ) .
• In the third quadrant, θ III = 180 ° + arctan ⁡ ( y x ) \theta_\text = 180° + \arctan(\frac) θ III ​ = 180° + arctan ( x y ​ ) .
• In the fourth quadrant, θ IV = 360 ° − arctan ⁡ ( y x ) \theta_\text = 360° - \arctan(\frac) θ IV ​ = 360° − arctan ( x y ​ ) .

🙋 The term arctan ⁡ ( y x ) \arctan(\frac) arctan ( x y ​ ) gives an angle in radians, and you must convert it to degrees before using it in the second, third, or fourth quadrant equations. Visit our angle conversion tool to learn how to do it.

How do I calculate a unit vector in the direction of another vector?

To find a unit vector û in the direction of another vector v = (x, y, z), follow these steps:

How do I find a vector of some magnitude in the direction of another?

To find a vector of a specific magnitude in the direction of another vector v = (x, y, z):

1. Find the magnitude of the vector v: |v| = √(x² + y² + z²)
2. Find a unit vector û in the direction of v. To do it, divide each coefficient of the vector v by the vector's magnitude: û = v/|v| = (x/|v|, y/|v|, z/|v|)
3. Multiply the magnitude of the desired vector by the unit vector û. That will result in the desired vector.

How do I find the magnitude and direction of two vectors?

To find the magnitude and direction of two vectors, you must find the resultant vector (you can use our vector addition calculator to do it) and apply to it the steps described above.

Now that you know how to find the magnitude and direction angle of a vector, let's look at some numerical examples and FAQs.

How do I find a vector of magnitude 3 in the direction of v = 12i - 5k?

To find a vector of magnitude 3 in the direction of v = 12i − 5k:

1. Find the magnitude of v: |v| = √(12² + (-5)²) = 13
2. Find a unit vector û in the direction of v. To do it, divide v by its magnitude: û = v/|v| = (12/13)i − (5/13)k
3. Multiply the desired magnitude 3 by the unit vector û. We obtain the vector w: w = 3û = (36/13)i − (15/13)k which has the desired direction and magnitude.

How do I calculate the unit vector in the direction of v = i + j + 2k

To calculate a unit vector in the direction of v = i + j + 2k:

1. Find the magnitude of v: |v| = √(1² + 1² + 2²) = √6 ≈ 2.4495
2. Divide the vector v by its magnitude: û = v/|v| = (1/√6)i + (1/√6)j + (2/√6)k
3. That's it. û is the unit vector in the direction of v.

Is the dot product of two vectors in the same direction positive or negative?

The dot product of two vectors in the same direction is always positive. That's because the dot product of two vectors in the same direction equals the multiplication of their magnitudes, and their magnitudes are always positive.

How do I find the magnitude and direction of two vectors' sum?

To find the magnitude and direction of two vectors' sum:

1. Find the resultant of the two vectors.
2. Sum the square of each of the components of the resultant vector.
3. Take the square root of the previous result, and this is the magnitude of your two vectors' sum!
4. To calculate the direction of the vector v = (x, y), use the formula θ = arctan(y/x), where θ is the smallest angle the vector forms with the horizontal axis, and x and y are the components of the resultant vector.